The Back-And-Forth Method (BFM) for Wasserstein Gradient Flows¶
This page provides documentation for the source code used in the paper The back-and-forth method for Wasserstein gradient flows [1]. A MATLAB wrapper to our C++ code is provided here: https://github.com/wonjunee/wgfBFMcodes.
Introduction¶
We are interested in simulating Darcy’s law (also known as the generalized porous medium equation)
on a domain Ω⊂R2. This equation describes the evolution of a mass density ρ flowing along a pressure gradient ∇ϕ generated by an energy functional U. The evolution of the density can be approximated by a discrete-in-time scheme known as the JKO scheme [3]. Given an initial density ρ(0), this scheme constructs approximate solutions by iterating
Here, τ plays the role of a time step and W2(⋅,⋅) is the 2-Wasserstein distance. We extend the back-and-forth method (BFM) [2] for optimal transport to efficiently solve (1). The BFM solves (1) via the dual formulation
where the supremum runs over functions ϕ,ψ:Ω→R satisfying
Installation¶
Requirements: FFTW (download here), MATLAB.
Clone or download the repository:
git clone https://github.com/wonjunee/wgfBFMcodes
cd wgfBFMcodes/
Compile: in a MATLAB session run
mex -O CFLAGS="\$CFLAGS -std=c++11" src/wgfslow.cpp -lfftw3
mex -O CFLAGS="\$CFLAGS -std=c++11" src/wgfinc.cpp -lfftw3
This will produce two MEX functions that you can use in MATLAB: wgfslow for slow diffusions and wgfinc for incompressible energies.
You may need to use -I and -L to link to the FFTW3 library, e.g. mex -O CFLAGS="\$CFLAGS -std=c++11" src/wgfslow.cpp -lfftw3 -I/usr/local/include. See this page for more information on how to compile MEX files.
Slow diffusion¶
Usage¶
In a MATLAB session, the command
rhoFinal = wgfslow(rhoInitial, V, obstacle, m, gamma, ...
maxIters, TOL, tau, nt, folder, verbose);
computes the JKO iterates ρ(n) from an initial density ρ(0) with the internal energy
The iterates ρ(n) will be stored as binary files rho-0000.dat, rho-0001.dat, etc in a user-specified folder.
Input:
rhoInitial: The nonnegative initial density ρ(0).V: The potential function V(x).obstacle: An obstacle in Ω. Any positive values indicate the obstacle. The densities ρ(n) will always be 0 on the obstacle.m: The constant m in the internal energy U.gamma: The constant γ in the internal energy U.maxIters: The maximum number of inner loop iterations k of the BFM in each outer iteration of the JKO scheme.TOL: The tolerance for the BFM. Once the error ‖Tϕk#ρ(n)−δU∗(ϕk)‖L1 becomes less than the tolerance, the algorithm stops the BFM and proceeds to the next outer iteration n+1.tau: The time step τ in (1).nt: The number of outer iterations n of the JKO scheme.folder: Path to the folder where the successive iterates ρ(n) will be saved. Don’t include a trailing slash.verbose:1- print out process inc++code.0- be silent.
Output:
rhoFinal: The final density ρ(nt) afterntouter iterations.
Example¶
We compute the Wasserstein gradient flow of a slow diffusion energy (3) on the 2d domain [0,1]2.
We discretize the problem on a 512×512 grid and plot the densities.
% Parameters
n = 512; % The size of the n x n grid
maxIters = 200; % Maximum number of BFM iterations
TOL = 1e-2; % Tolerance for BFM
nt = 60; % Number of outer iterations
tau = 0.005; % Time step in the JKO scheme
m = 2; % m in the internal energy
gamma = 0.05; % gamma in the internal energy
folder = 'data'; % Output directory
verbose = 1; % pPrint out logs
[x,y] = meshgrid(linspace(0,1,n));
% Initial density
rhoInitial = zeros(n);
idx = (x-0.5).^2 + (y-0.5).^2 < 0.1^2;
rhoInitial(idx) = 1;
rhoInitial = rhoInitial / sum(rhoInitial(:)) * n^2;
% Potential
V = sin(3*pi*x) .* sin(3*pi*y);
% No obstacle
obstacle = zeros(n);
% Plots
subplot(1,2,1)
contourf(x, y, rhoInitial)
title('Initial density')
axis square
subplot(1,2,2)
contourf(x, y, V);
title('Potential V')
axis square
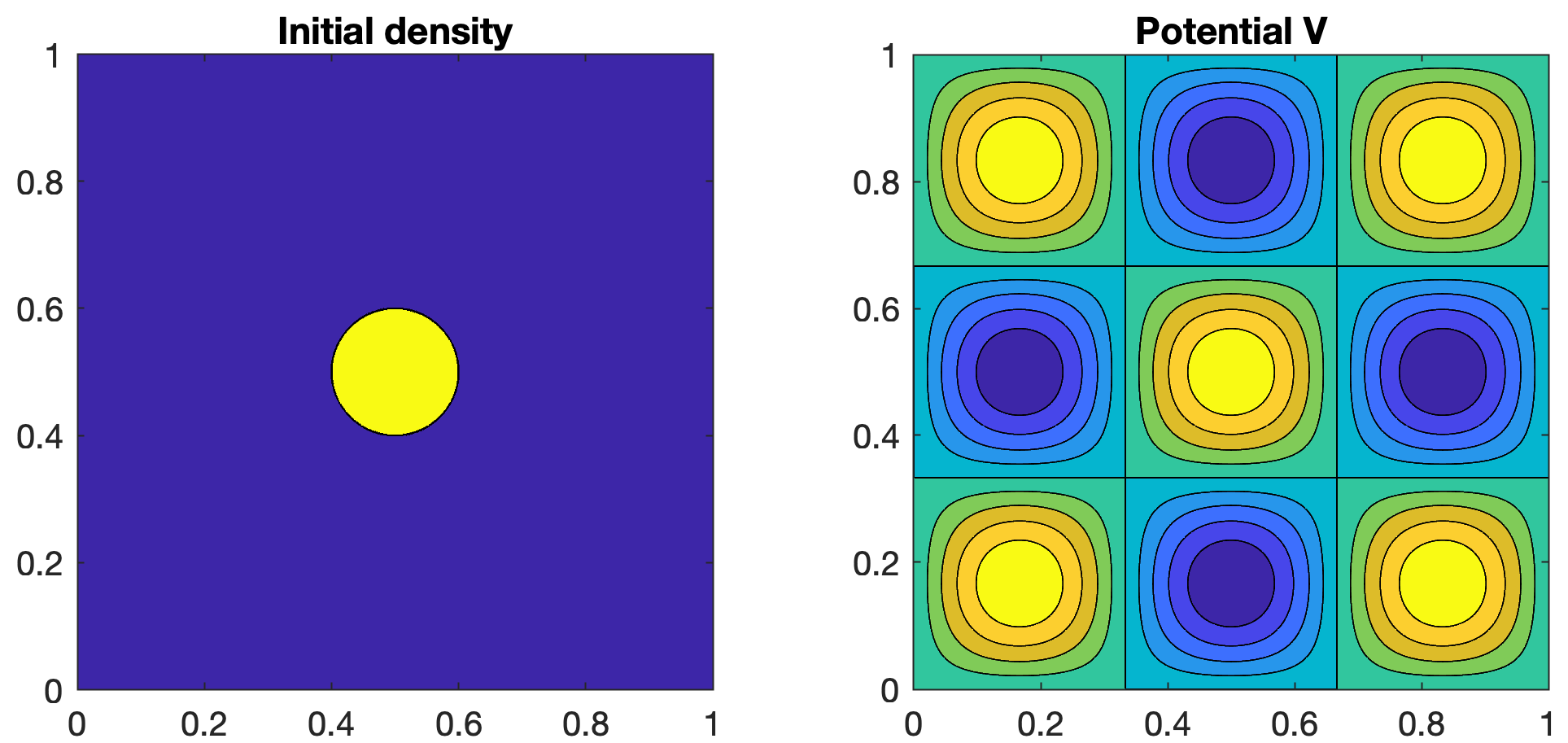
Here ρ(0) is renormalized so that ∫Ωρ(0)(x)dx=1. Now run the algorithm
rhoFinal = wgfslow(rhoInitial, V, obstacle, m, gamma, ...
maxIters, TOL, nt, tau, folder, verbose);
Output:
XXX Slow Diffusion XXX
n : 512
nt : 60
tau : 0.005
m : 2
gamma: 0.05
Max Iteration : 200
Tolerance : 0.01
CPU time for FFT: 0.005817 seconds.
The total mass : 1
Iter : 1
50 Dual value: 1.2282 L1 error: 0.0262
100 Dual value: 1.2280 L1 error: 0.0193
150 Dual value: 1.2279 L1 error: 0.0172
...
Iter : 60
1 Dual value: -0.2241 L1 error: 0.0024
CPU time for GF: 70.906929 seconds.
Make movie
fig = figure;
movieName = 'movie.gif';
for i = 0:nt
file = fopen(sprintf("%s/rho-%04d.dat", folder, i), 'r');
rho = fread(file, [n n], 'double');
imagesc(rho)
axis xy square
set(gca,'XTickLabel',[], 'YTickLabel',[])
frame = getframe(fig);
im = frame2im(frame);
[X,cmap] = rgb2ind(im, 256);
% Write to the GIF file
if i == 0
imwrite(X, cmap, movieName, 'gif', 'Loopcount',inf, 'DelayTime',0.03);
else
imwrite(X, cmap, movieName, 'gif', 'WriteMode','append', 'DelayTime',0.03);
end
end
The file movie.gif

Incompressible energy¶
Usage¶
In a MATLAB session, the command
rhoFinal = wgfinc(rhoInitial, V, obstacle, maxIters, TOL, ...
tau, nt, folder, verbose);
computes the JKO iterates ρ(n) from an initial density ρ(0) with the internal energy
Here u∞(ρ)=0 if 0≤ρ≤1 and +∞ otherwise.
The iterates ρ(n) will be stored as binary files rho-0000.dat, rho-0001.dat, etc in a user-specified folder.
Input:
rhoInitial: The nonnegative initial density ρ(0).V: The potential function V(x).obstacle: An obstacle in Ω. Any positive values indicate the obstacle. The densities ρ(n) will always be 0 on the obstacle.maxIters: The maximum number of inner loop iterations k of the BFM in each outer iteration of the JKO scheme.TOL: The tolerance for the BFM. Once the error ‖Tϕk#ρ(n)−δU∗(ϕk)‖L1 becomes less than the tolerance, the algorithm stops the BFM and proceeds to the next outer iteration n+1.tau: The time step τ in (1).nt: The number of outer iterations n of the JKO scheme.folder: Path to the folder where the successive iterates ρ(n) will be saved. Don’t include a trailing slash.verbose:1- print out process in C++ code.0- be silent.
Output:
rhoFinal: The final density ρ(nt) afterntouter iterations.
Example¶
We compute the Wasserstein gradient flow of an incompressible energy (4) on the 2d domain [0,1]2.
We discretize the problem on a 512×512 grid and plot the densities.
n = 512; % The size of the n x n grid
maxIters = 300; % Maximum number of BFM iterations
TOL = 3e-2; % Tolerance for BFM
nt = 180; % Number of outer iterations
tau = 0.005; % Time step in the JKO scheme
folder = 'data'; % Output directory
verbose = 1; % Print out logs
[x,y] = meshgrid(linspace(0,1,n));
% Initial density
rhoInitial = zeros(n);
idx = (x-0.25).^2 + (y-0.75).^2 < 0.15^2;
rhoInitial(idx) = 1;
% Potential
V = 3 * ((x-0.7).^2 + (y-0.3).^2);
% Add an obstacle
obstacle = zeros(n);
idx = (x-0.5).^2 + (y-0.5).^2 < 0.1^2;
obstacle(idx) = 1;
% Plots
subplot(1,3,1)
contourf(x, y, rhoInitial)
title('Initial density')
axis('square')
subplot(1,3,2)
contourf(x, y, V);
title('Potential V')
axis('square')
subplot(1,3,3)
contourf(x, y, obstacle)
colormap(gca, 'copper')
title('Obstacle')
axis('square')
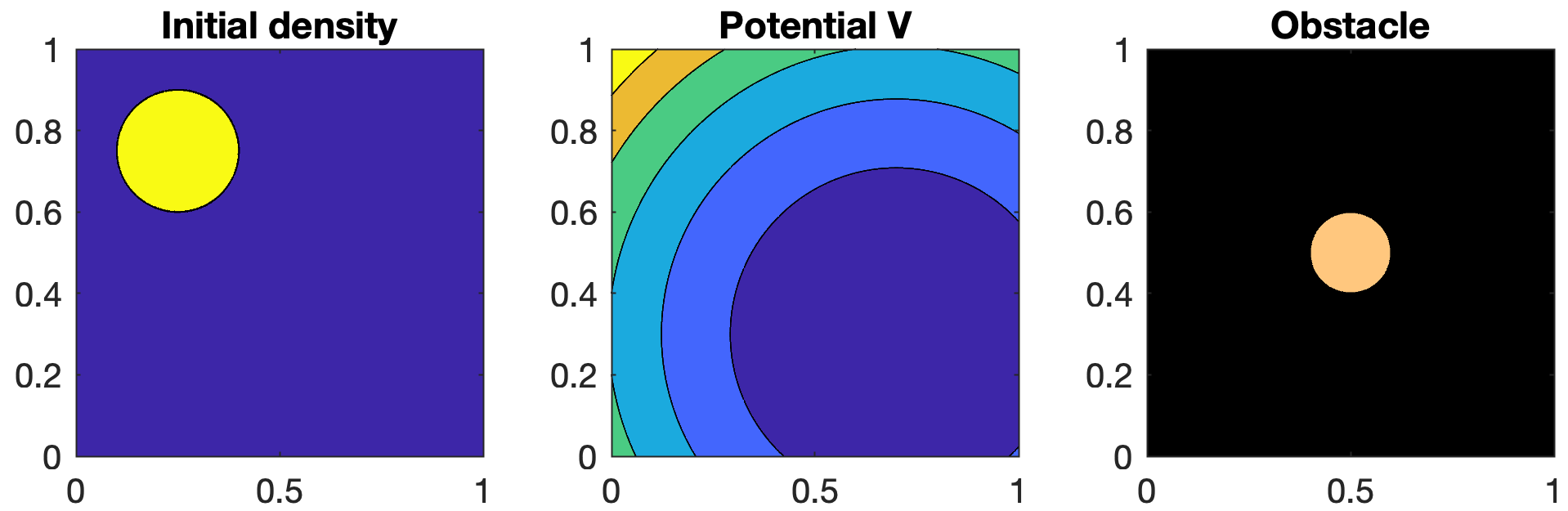
Run the algorithm
rhoFinal = wgfinc(rhoInitial, V, obstacle, maxIters, TOL, nt, tau, ...
folder, verbose);
Output:
XXX Incompressible Flow XXX
n : 512
nt : 180
tau : 0.005
Max Iteration : 300
Tolerance : 0.03
CPU time for FFT: 0.295334 seconds.
Total mass : 0.0703964
Iter : 1
10 dual value: 0.085350 L1 error: 0.1135
20 dual value: 0.085378 L1 error: 0.0807
30 dual value: 0.085386 L1 error: 0.0628
40 dual value: 0.085390 L1 error: 0.0525
50 dual value: 0.085391 L1 error: 0.0446
56 dual value: 0.085392 L1 error: 0.0407
...
Iter : 180
7 dual value: 0.002379 L1 error: 0.0329
CPU time for GF: 616.0 seconds.
Note that here there is a ceiling contraint ρ(x)≤1 so the total mass must be less than 1. Make movie
fig = figure;
movieName = 'movie.gif';
for i = 0:nt
file = fopen(sprintf("%s/rho-%04d.dat", folder, i), 'r');
rho = fread(file, [n n], 'double');
imagesc(rho)
axis xy square
set(gca,'XTickLabel',[], 'YTickLabel',[])
frame = getframe(fig);
im = frame2im(frame);
[X,cmap] = rgb2ind(im, 256);
% Write to the GIF file
if i == 0
imwrite(X, cmap, movieName, 'gif', 'Loopcount',inf, 'DelayTime',0.001);
else
imwrite(X, cmap, movieName, 'gif', 'WriteMode','append', 'DelayTime',0.001);
end
end
The file movie.gif

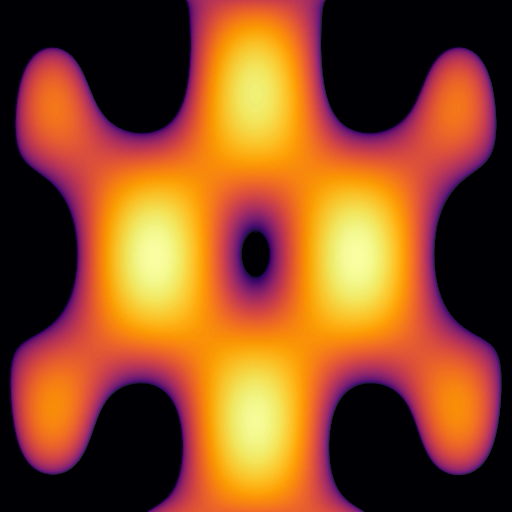
More Videos¶
Here are other cool things you can do with the BFM.
Slow diffusion flow with m=4, a quadratic potential and a star-shaped obstacle. (512 x 512 pixels)
Slow diffusion flow with potential V(x)=−sin(5πx1)sin(3πx2). Top: m=2. Bottom: m=4. (512 x 512 pixels)
Aggregation-diffusion: slow diffusion + a concave interaction kernel. (512 x 512 pixels)
Incompressible flow. (1024 x 1024 pixels)
Moving obstacles and moving potential. (512 x 512 pixels)
References¶
[1] Matt Jacobs, Wonjun Lee, and Flavien Léger. The back-and-forth method for Wasserstein gradient flows. Submitted. 2020.
[2] Matt Jacobs and Flavien Léger. A fast approach to optimal transport: the back-and-forth method. Numerische Mathematik (2020): 1-32.
[3] Richard Jordan, David Kinderlehrer, and Felix Otto. The variational formulation of the Fokker–Planck equation. SIAM journal on mathematical analysis (1998): 29(1), 1–17.